1. 이진 탐색 (Binary Search)
- 정렬된 배열에서 값을 효율적으로 찾는 알고리즘
- 배열의 중간 요소를 선택하고, 찾고자 하는 값과 비교하는 과정이 반복된다
- 과정:
- 중간 요소와 찾고자 하는 값을 비교
- 중간 값이 찾는 값보다 크면 왼쪽 절반으로, 작으면 오른쪽 절반으로 검색 범위를 좁힌다
- 이 과정을 범위가 하나의 요소로 좁혀질 때까지 반복하거나, 찾는 값이 없다고 판별될 때까지 반복한다
- 시간 복잡도는 O(logn)을 보장하며, 정렬된 데이터에서 빠르게 값을 찾을 수 있다.
- 이진 탐색은 배열이나 리스트와 같은 선형 자료구조에서 주로 사용된다.
2. 이진 탐색 트리 (Binary Search Tree, BST)
- 이진 탐색 트리는 이진 트리의 특수한 형태로, 모든 노드가 특정 정렬 기준에 맞게 정렬되어 있다.
- 특징:
- 각 노드의 왼쪽 서브트리에는 해당 노드보다 작은 값들이, 오른쪽 서브트리에는 해당 노드보다 큰 값들이 위치한다.
- 이진 탐색 트리는 이진 탐색의 논리를 트리 자료구조에 적용한 것이다
- 이진 탐색 수행:
- BST에서는 원하는 값을 찾기 위해 루트에서 시작하여, 값을 비교하면서 왼쪽이나 오른쪽으로 내려가는 방식으로 이진 탐색을 수행할 수 있다.
- BST를 통해 삽입, 삭제, 탐색 작업을 효율적으로 수행할 수 있다. 최적의 경우에는 시간 복잡도가 O(logn)이지만, 트리가 편향되면 최악의 경우 O(n)이 될 수 있다.
(1)
다음과 같이 정렬된 데이터에서 이진탐색을 수행하는 경우 비교 횟수가 가장 많은 데이터는?
(단, 배열의 인덱스는 내림 함수를 적용하여 구한다)
| 4 6 11 12 15 17 18 20 21 |
중간 위치 인덱스를 구할 때는 low와 high를 더하고 2로 나눈다.
단, 소수점이 발생할 경우 문제에서 요구한대로 내림 함수를 적용한다.
데이터의 개수가 아홉개 이므로 임의의 값 탐색 성공에 있어 비교횟수 4를 넘지 않는다.
맨 처음 탐색 범위가 전체 데이터일때 low(1)과 high(9)를 더해 2로 나눈다.
가장 먼저 탐색하게 되는 인덱스는 5가 된다. 탐색하고자 하는 값과 5번 인덱스의 값 15와 비교하여
작으면 1부터 4, 크면 6부터 9 범위에서 다시 탐색한다.
| 탐색성공 | 3 | 2 | 3 | 4 | 1 | 3 | 2 | 3 | 4 |
| 비교횟수 | 4 | 6 | 11 | 12 | 15 | 17 | 18 | 20 | 21 |
| [1] | [2] | [3] | [4] | [5] | [6] | [7] | [8] | [9] |
가장 많은 데이터 : 12, 21
(2)
다음의 정렬된 데이터에서 2진탐색을 수행하여 C를 찾으려고 한다.
몇 번의 비교를 거쳐야 C를 찾을 수 있는가?
(단, 비교는 크다, 작다, 같다 중의 하나로 수행되고 같다가 도출될 때까지 반복된다)
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O |
| [0] | [1] | [2] | [3] | [4] | [5] | [6] | [7] | [8] | [9] | [10] | [11] | [12] | [13] | [14] |
| 4 | 3 | 4 | 2 | 1 |
답 : 4번
(3)
탐색 성능(시간 복잡도)
| 탐색 방법 | 시간 복잡도 |
| 순차 탐색 | O(n) |
| 제어 탐색 - 이진 탐색 | O(logn) |
| 이진 탐색 트리 | 균형 : O(logn), 불균형 : O(n) |
| AVL 트리 | O(logn) |
| 해싱 | 완전 해싱 : O(1), 충돌 발생 : O(n) |
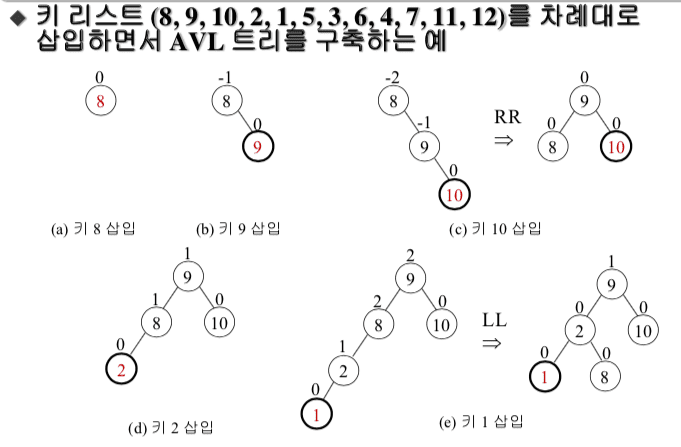
3. 해싱의 주요 개념
해싱(Hashing)은 데이터를 고정된 크기의 해시 값(Hash Value)으로 변환하는 과정으로, 빠른 데이터 검색과 저장을 위해 주로 사용된다.
해싱은 특히 해시 테이블(Hash Table)이라는 자료 구조에서 데이터 삽입, 삭제, 검색을 효율적으로 수행하는 핵심 원리이다
- 해시 함수 (Hash Function)
- 해시 함수는 입력값을 특정 규칙에 따라 고정된 길이의 해시 값으로 변환한다. 이름이나 키와 같은 데이터를 해시 함수에 넣으면 특정한 숫자나 문자열로 변환된다.
- 해시 함수의 이상적인 특성은 빠르고 효율적이며, 서로 다른 입력이 같은 해시 값을 가질 가능성이 낮아야 한다.
- 해시 값 (Hash Value)
- 해시 함수가 만들어낸 결과 값이다. 주어진 입력에 대해 고유한 해시 값을 반환해줘서, 해시 값을 통해 데이터가 어디에 저장되어 있는지 빠르게 찾을 수 있다.
- 예를 들어, 문자열 "apple"을 해시 함수에 넣으면 고정된 길이의 숫자나 문자열(예: 4521)이 반환된다. 이 해시 값은 해시 테이블에서 특정한 위치를 가리키는 역할을 한다.
- 해시 테이블 (Hash Table)
- 해시 테이블은 키와 값을 저장하는 자료 구조로, 각 데이터의 위치를 해시 함수로 결정한다. 해시 테이블은 평균적으로 O(1)의 시간 복잡도로 빠르게 데이터를 검색하고 삽입할 수 있다.
- 해시 테이블은 배열과 유사한 구조로, 특정 키에 대한 해시 값을 배열의 인덱스로 사용해 데이터를 저장하거나 검색한다.
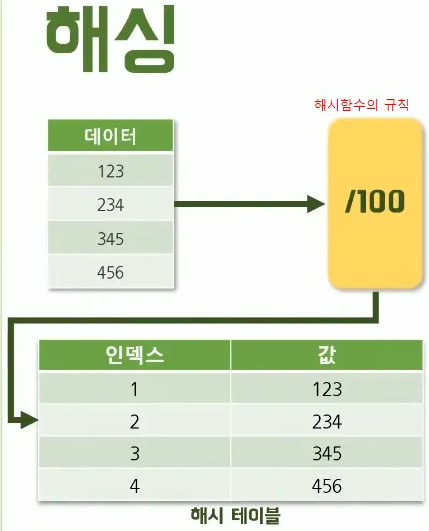
- 해시에서 데이터를 보고 규칙적으로 뿌려주는 것이 해시 함수 (더하기, 빼기, 곱하기, 모듈, 비트연산 등등)
- 데이터가 해시함수를 거쳐 분류된 이후 정보가 저장되는 것이 해시 테이블
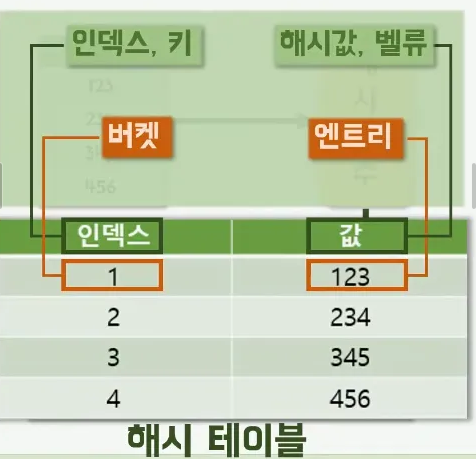
- 해시 테이블의 첫번째 컬럼은 인덱스(키), 두번째 컬럼은 값(밸류) 가 저장된다.
- 안에 인덱싱 된 기준이 버켓, 그 안의 값을 엔트리라고 한다
즉, 데이터들이 오면 해시 함수에 의해 분류가 되고 규칙에 의해 해시 테이블 안에 예쁘게 들어가며
이 모든 과정을 해싱이라고 한다
(1)
해싱 탐색에서 제산법은 키 값을 배열의 크기로 나누어 그 나머지 값을 해시 값으로 사용하는 방법이다.
다음 데이터의 해시 값을 제산법으로 구하여 11개의 원소를 갖는 배열에 저장하려고 한다.
해시 값의 충돌이 발생하는 데이터를 열거해 놓은 것은?
| 111, 112, 113, 220, 221, 222 |
제산법은 나눈 나머지로 주소 값을 정한다. 해시 주소가 같으면 충돌이 발생한 것이다.
각 키의 해시 주소를 구하면 다음과 같다
- 111 % 11 = 1
- 112 % 11 = 2
- 113 % 11 = 3
- 220 % 11 = 0
- 221 % 11 = 1
- 222 % 11 = 2
111과 221이 충돌, 112와 222가 충돌이 발생하였다.
(2)
전화번호의 마지막 네 자리를 3으로 나눈 나머지를 해싱하여 데이터베이스에 저장하고자 한다.
나머지 셋과 다른 저장 장소에 저장되는 것은?
010-4021-6718
010-9615-4815
010-7290-6027
010-2851-5232
마지막 네 자리를 3으로 나눈 나머지가 해시주소가 된다
- 6718 % 3 = 1
- 4815 % 3 = 0
- 6027 % 3 = 0
- 5232 % 3 = 0
즉 6718번만 나머지와 다르다
(3)
해싱과 오버플로우
해싱 기법의 키 공간 T는 버킷의 수보다 매우 크고 한 버킷의 슬롯 수는 적으므로 오버플로우가 필연적으로 발생하게 되어, 오버플로우를 처리하는 기법이 필요하게 된다.
- 개방 주소법 : 선형조사법, 이차조사법, 이중해싱, 재해싱 등이 해당되며 이들은 처음에 구해진 해시주소를 다시 계산하여 오버플로우를 해결한다
- 폐쇄 주소법 : 처음 구해진 해시 주소를 변경하지 않고 연결리스트를 사용하며 체이닝(chaining)이 이에 해당한다
해싱 기법에는 숫자분석법, 제산법, 제곱법, 접지법(폴딩함수) 등이 있다
(4)
해시 함수로 h(k) = k mod 7을 사용하고, 선형 탐색 기법을 이용하여 충돌을 해결하고자 한다.
키가 3, 10, 5, 9, 12 순서대로 입력되었을 때 생성된 해시 테이블은?
해시 함수는 제산법이므로 7로 나눠 구해진 나머지가 해시 주소가 된다.
충돌이 발생하면 선형 탐색에 의해 새로운 주소를 구한다.
원래의 주소에 +1하고, 또 충돌이 나면 원래의 주소에 +2... 를 하여 저장할 수 있는 해시 주소를 구하면 된다.
3%7 = 3
10%7 = 3, 충돌이 발생했으므로 선형 탐색에 의해 새로운 해시주소는 3+1인 4가 된다.
5%7 = 5
9%7=2
12%7=5, 충돌이 발생했으므로 선형 탐색에 의해 새로운 해시주소는 5+1인 6이 된다.
| [0] | [1] | [2] | [3] | [4] | [5] | [6] |
| 9 | 3 | 10 | 5 | 12 |
4. 이진 탐색과 해싱
이진 탐색과 해싱은 둘 다 데이터 검색을 빠르게 수행하기 위한 방법이라는 공통점이 있다.
하지만, 각각의 접근 방식과 활용되는 구조가 다르기 때문에 서로 다른 상황에 유리하다.
공통점
- 효율적인 데이터 검색:
- 두 방법 모두 데이터를 빠르게 찾기 위해 설계되었다. 일반적으로 선형 탐색보다 훨씬 빠르게 원하는 데이터를 찾을 수 있다.
- 시간 복잡도 감소:
- 이진 탐색은 정렬된 배열에서 O(logn)의 시간 복잡도로 작동하고, 해싱은 평균적으로 O(1)의 시간 복잡도로 데이터를 찾을 수 있다. 이로 인해 데이터 크기가 커져도 상대적으로 빠른 검색이 가능하다
- 특정 값에 대한 빠른 접근:
- 이진 탐색은 배열에서 중간 값을 기준으로 데이터를 반씩 줄여가며 접근하고, 해싱은 키를 해시 값으로 변환하여 특정 인덱스로 직접 접근한다. 두 방법 모두 특정 데이터를 빠르게 찾기 위해 직접 접근 방식을 사용한다.
차이점
- 사용되는 자료구조:
- 이진 탐색은 정렬된 배열이나 리스트에서 사용되는 반면, 해싱은 해시 테이블을 사용함
- 검색 조건:
- 이진 탐색은 데이터를 검색하려면 정렬되어 있어야 하지만, 해시는 정렬과 상관없이 작동함
- 시간 복잡도:
- 이진 탐색은 O(logn)으로 작동하지만, 해싱은 이상적인 경우 O(1)로 더 빠르게 작동함
- 최악의 경우 이진탐색은 동일하게 O(logn)이지만 해싱은 O(n)으로 이진 탐색보다 느리다
'컴퓨터 일반 > 자료구조론' 카테고리의 다른 글
| 자료구조 문제 정리 (5) 정렬 (0) | 2024.10.29 |
|---|---|
| 자료구조 문제 정리 (4) 그래프 (3) | 2024.10.29 |
| 자료구조 문제 정리 (3) 트리 (0) | 2024.10.25 |
| 자료구조 문제 정리 (2) 스택, 큐 (0) | 2024.10.25 |
| 자료구조 문제 정리 (1) 배열, 리스트 (4) | 2024.10.25 |


