정렬 알고리즘 시간 복잡도
| 정렬종류 | 평균 | 최악 |
| 버블정렬 | O(n^2) | O(n^2) |
| 선택정렬 | O(n^2) | O(n^2) |
| 삽입정렬 | O(n^2) | O(n^2) |
| 퀵정렬 | O(nlogn) | O(n^2) |
| 2-way merge 정렬 | O(nlogn) | O(nlogn) |
| 힙 정렬 | O(nlogn) | O(nlogn) |
| 기수 정렬 | O(n) | O(n) |
*삽입 정렬과 버블 정렬의 경우 이미 정렬된 입력 데이터로 O(n)의 시간복잡도를 얻을 수 있다
1. 버블 정렬(Bubble sort)
버블 정렬은 가장 기본적인 알고리즘 중 하나로, 인접한 데이터와 비교하면서 가장 큰 데이터를 맨 뒤로 옮긴다.
맨 뒤에서부터 저장을 완료해나가는 방식이다
안정적인 정렬이다.
void Bubble_Sort(int arr[], int len) {
int i, j, tmp;
for (i = 0; i < len - 1; ++i) {
for (j = 0; j < len - i - 1; ++j) {
if (arr[j] > arr[j + 1]) { //오름차순
tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
}
}
}
}오름차순 정렬일 경우 arr[j] > arr[j+1]
내림차순 정렬일 경우 arr[j] < arr[j+1]
인접한 데이터와 비교하기 때문에 첨자는 j+1이다.
(1)
다음 자료를 버블 정렬 알고리즘을 적용하여 오름차순으로 정렬할 때,
세번째 패스까지 실행한 정렬 결과로 옳은 것은?
| 5, 2, 3, 8, 1 |
인접한 데이터와 비교하여 정렬한다
2 5
2 3 5
2 3 5 8
2 3 5 1 8 <- 1 pass한 결과이다, 뒤에서부터 큰 숫자대로 정렬된다.
- 1 pass : 2 3 5 1 8
- 2 pass : 2 3 1 5 8
- 3 pass : 2 1 3 5 8
(2)
입력값으로 5,2,3,1,8이 주어졌을 때 버블정렬의 1회전 결과는?
2 3 1 5 8
(3)
버블 정렬에 대한 의사코드
| Function(A[ ], n) { for last <- n downto 2 //last를 n에서 2까지 1씩 감소 for i <- 1 to last -1 if (A[i] > A[i+1]) then A[i] <-> A[i+1]; // A[i]와 A[i+1]를 교환 } |
| 제일 큰 원소를 끝자리로 옮기는 작업을 반복한다 O(n^2)의 수행 시간을 가진다 두번째 for 문의 역할은 가장 큰 원소를 맨 오른쪽으로 보내는 것이다 |
2. 선택 정렬(Selection sort)
- 가장 단순한 정렬 시리즈 중 하나
- 가장 작은 숫자를 차례대로 탐색, 가장 왼쪽 자리부터 스왑
- 가장 작은 숫자를 선택하는 방식이라서 선택 정렬이다.
- 제일 작은 숫자부터 왼쪽으로 최종 위치 확정
void selectionSort(int *list, const int n)
{
int i, j, indexMin, temp;
for (i = 0; i < n - 1; i++)
{
indexMin = i;
for (j = i + 1; j < n; j++)
{
if (list[j] < list[indexMin])
{
indexMin = j;
}
}
temp = list[indexMin];
list[indexMin] = list[i];
list[i] = temp;
}
(1)
다음 수를 선택 정렬로 오름차순 할 경우, Pass 2를 진행한 후의 결과로 옳은 것은?
| 10, 3, 5, 9, 6, 8 |
선택정렬의 오름차순은 비교 데이터 중 가장 작은 값을 골라 맨 앞의 데이터와 교환한다.
1 pass : 3 10 5 9 6 8
2 pass : 3 5 10 9 6 8
(2)
다음 동작에 해당하는 정렬 방법은?
| 정렬할 원소 : 34 27 19 50 2 21 16 1단계 : 2 27 19 50 34 21 13 2단계 : 2 13 19 50 34 21 27 3단계 : 2 13 19 50 34 21 27 4단계 : 2 13 19 21 34 50 27 5단계 : 2 13 19 21 27 50 34 6단계 : 2 13 19 21 27 34 50 |
최솟값을 찾아 첫번재 원소와 교환하였으므로 선택 정렬이다
(3)
다음과 같이 수행되는 정렬 알고리즘으로 옳은 것은?
| 단계 0 : 6 5 8 9 4 2 단계 1 : 6 5 8 2 4 9 단계 2 : 6 5 4 2 8 9 단계 3 : 2 5 4 6 8 9 단계 4 : 2 4 5 6 8 9 단계 5 : 2 4 5 6 8 9 |
한 단계에서 가장 최대값을 찾아 가장 오른쪽 값과 교환하는 선택 정렬이다.
3. 삽입 정렬(Insert sort)
- 가장 기본적인 정렬 중 하나
- 정렬된 어레이를 유지하며 진행
- 점점 사이즈를 키워가는 방식, 정렬된 작은 어레이를 크기를 한칸씩 늘려가면서 진행함
- 새로운 숫자가 삽입되면 정렬된 어레이 안에서 자기의 자리를 찾아가며 정렬
- 최종 위치가 확정되는 것이 없음
void insertion_sort ( int *data, int n )
{
int i, j, remember;
for ( i = 1; i < n; i++ )
{
remember = data[(j=i)];
while ( --j >= 0 && remember < data[j] ){
data[j+1] = data[j];
}
data[j+1] = remember;
}
}
(1)
다음 자료를 오름차순으로 삽입 정렬하는 과정은?
| 3, 1, 4, 2, 9, 5 |
초기 상태 : 3 1 4 2 9 5
1회전 : 1 3 4 2 9 5
2회전 : 1 3 4 2 9 5
3회전 : 1 2 3 4 9 5
4회전 : 1 2 3 4 9 5
5회전 : 1 2 3 4 5 9
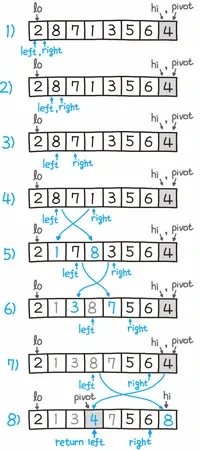
4. 퀵 정렬
- 분할 정복(divide and conquer) 정렬 방법 중 하나로 평균 시간 복잡도가 O(nlogn)이다.
- 분할 정복 알고리즘(Divide and conquer algorithm)은 그대로 해결할 수 없는 문제를 작은 문제로 분할하여 문제를 해결하는 방법이나 알고리즘이다.
- 평균수행시간이 비교에 의한 정렬 방법 중에서 가장 짧다
- 배열 내의 한 원소를 피봇(pivot)으로 정한다.
- 이 피봇을 기준으로 배열 내의 원소들을 두 개의 부파일로 분할한다.
- 왼쪽 분할은 이 피봇보다 작은 값의 원소들로 구성된다.
- 오른쪽 분할은 이 피봇보다 큰 값의 원소들로 구성된다.
- 퀵 정렬 알고리즘은 이 왼쪽 분할과 오른쪽 분할에 대해 다시 퀵정렬을 순환적으로 수행한다.
- 이 순환 반복은 각 분할이 하나의 원소 이하로 될 때까지 계속한다.
- 수행과정에서 순환 알고리즘을 사용하므로 스택이 필요하다 (재귀 함수 호출)
- 평균 수행시간은 O(nlogn)이고, 최악은 O(n^2)이다
- 정렬된 입력 데이터에 대해 최악의 시간 복잡도를 가지게 된다.
- 원소들 중에 같은 값이 있는 경우 같은 값들의 정렬 이후 순서가 초기 순서와 달라질 수 있어 불안정 정렬에 속한다.
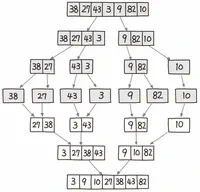
5. 병합 정렬/합병 정렬(merge sort)
- 분할 정복 알고리즘 : 분할한 다음 다시 합치는 과정으로 정렬을 수행한다
- 모든 숫자를 다 나눈 다음에 병합하는 방식으로 정렬 진행
- 그룹끼리 합쳐지면서 더 큰 그룹이 만들어진다
- 2개 이상의 파일의 값들을 비교하여 정렬하여 하나의 파일로 합병하는 기법이며 평균, 최악의 경우 시간 복잡도가 모두 O(nlogn)으로 데이터의 정렬 상태에 영향을 받지 않는다
- 주어진 배열의 크기와 같은 임시 배열을 추가로 만들어야 하기 때문에 다른 정렬기법에 비해 기억공간을 많이 사용한다
- 대량의 데이터를 대상으로 테이프나 디스크를 이용하는 경우 사용하기도 한다
(1)
다음은 데이터가 정렬되는 단계를 일부 보여준 것이다.
어떤 정렬 알고리즘을 사용하면 이와 같은 데이터 자리 교환이 일어나겠는가?
| 초기 데이터 | 8 9 4 3 7 1 5 2 3 9 3 4 1 7 2 5 3 4 8 9 1 2 5 7 |
| 정렬 데이터 | 1 2 3 4 5 7 8 9 |
합병 정렬은 2개의 파일을 합하여 1개의 정렬된 파일을 구한다.
가장 최종적으로 한 개의 정렬 파일을 얻게 되면 정렬이 종료된다
- 초기 : 8 / 9 / 4 / 3 / 7 / 1 / 5 / 2
- 1단계 정렬 : 8 9 / 3 4 / 1 7 / 2 5
- 2단계 정렬 : 3 4 8 9 / 1 2 5 7
- 정렬 완성 : 1 2 3 4 5 7 8 9
6. 기수 정렬 (radix sort)
- 비교가 아닌 분배에 의한 정렬 방식이다
- 정렬할 원소의 키 값을 나타내는 숫자의 자리 수(radix)를 기초로 정렬하는 기법이다.
- 정렬할 키의 가장 작은 자리 수(LSD)를 기준으로 분배하여 정렬한다.
- 다음에는 첫번째 패스의 결과를 두번째로 작은 자리수를 기준으로 다시 분배하여 정렬한다
- 이러한 정렬 과정을 키의 제일 큰 자리수까지 반복해서 수행하면 최종적으로 원하는 정렬 결과를 얻게 된다
'컴퓨터 일반 > 자료구조론' 카테고리의 다른 글
| 자료구조 문제 정리 (6) 탐색, 해싱 (0) | 2024.10.29 |
|---|---|
| 자료구조 문제 정리 (4) 그래프 (3) | 2024.10.29 |
| 자료구조 문제 정리 (3) 트리 (0) | 2024.10.25 |
| 자료구조 문제 정리 (2) 스택, 큐 (0) | 2024.10.25 |
| 자료구조 문제 정리 (1) 배열, 리스트 (4) | 2024.10.25 |


