알고리즘 빅오 표기법
컴퓨터가 하는 일 : 데이터 저장, 연산
어떻게 하면 데이터를 적은 메모리에 저장할까? → 자료구조
어떻게 하면 문제를 빠르고 정확하게 해결할 수 있을까? → 알고리즘
알고리즘의 효율성을 판단하는 근거로 시간 복잡도와 공간 복잡도를 들 수 있다.
- 시간 복잡도 : 얼마나 빠르게 결과를 출력할수 있을까? T(n)
- 공간 복잡도 : 메모리를 얼마나 사용하는가? S(n)
효율성을 판단하는 표기법으로 빅오 표기법, 빅오메가 표기법, 빅세타 표기법이 있다.
빅오 표기법
최악일 때의 성능을 판단하는 것이다. 이보다 더 나쁜 경우는 없어를 기준으로 한다 (상한)
가장 많이 사용하는 분석방법이다 ↔ 최상일 때의 경우를 판단하는 것은 빅오메가 표기법이다.
시간 복잡도
시간 복잡도는 문제를 해결하는데 몇번의 단계를 거쳐야 하는지로 판별한다. (연산의 횟수, 문제 수행 단계로 복잡도 판단)

- O(1) = 항상 같은 시간 복잡도
- log(N) = 1/2 시간 복잡도 *데이터의 양이 많아질수록 효율적
- O(N) = 선형 시간을 보장 받는 시간복잡도

접근적 표기법이란?
- 상수 값은 떼어버린다 : ex) O(3N) 이라면 O(N)으로 표기
- 최고차항만을 남긴다 : O(5N^2 + N) → O(N^2)
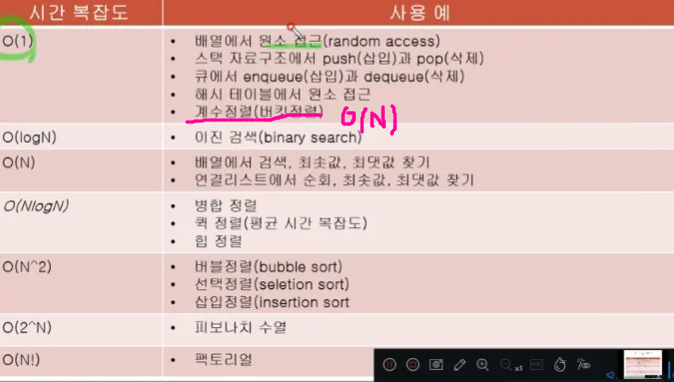

데이터의 양이 많아질수록 속도 차이가 많이 난다.
https://www.youtube.com/watch?v=UOsEmxxPfyA 강의를 참고하여 작성하였습니다
EX. 입력 데이터 개수 N에 대한 시간 복잡도가 가장 큰 것은?
- O(10(n+logn))
- O(n^2+1)
- O(3nlogn+100)
- O(n^2logn)
알고리즘의 기본 연산수를 구하는 것은 각 연산의 수행 빈도수를 합한 것으로 정한다.
만일 그 연산수가 여러 개의 다른 항으로 표현되어 있다면 그 중 차수가 제일 높은 것을 선택한다
- O(10(n+logn)) = O(N)
- O(n^2+1) = O(N^2)
- O(3nlogn+100) = O(nlogn)
- O(n^2logn) = O(n^2logn)
O(1) < O(log2N) < O(n) < O(log2N) < O(N^2) < O(N^3) < O(2^n) < O(n!) < O(n^n)
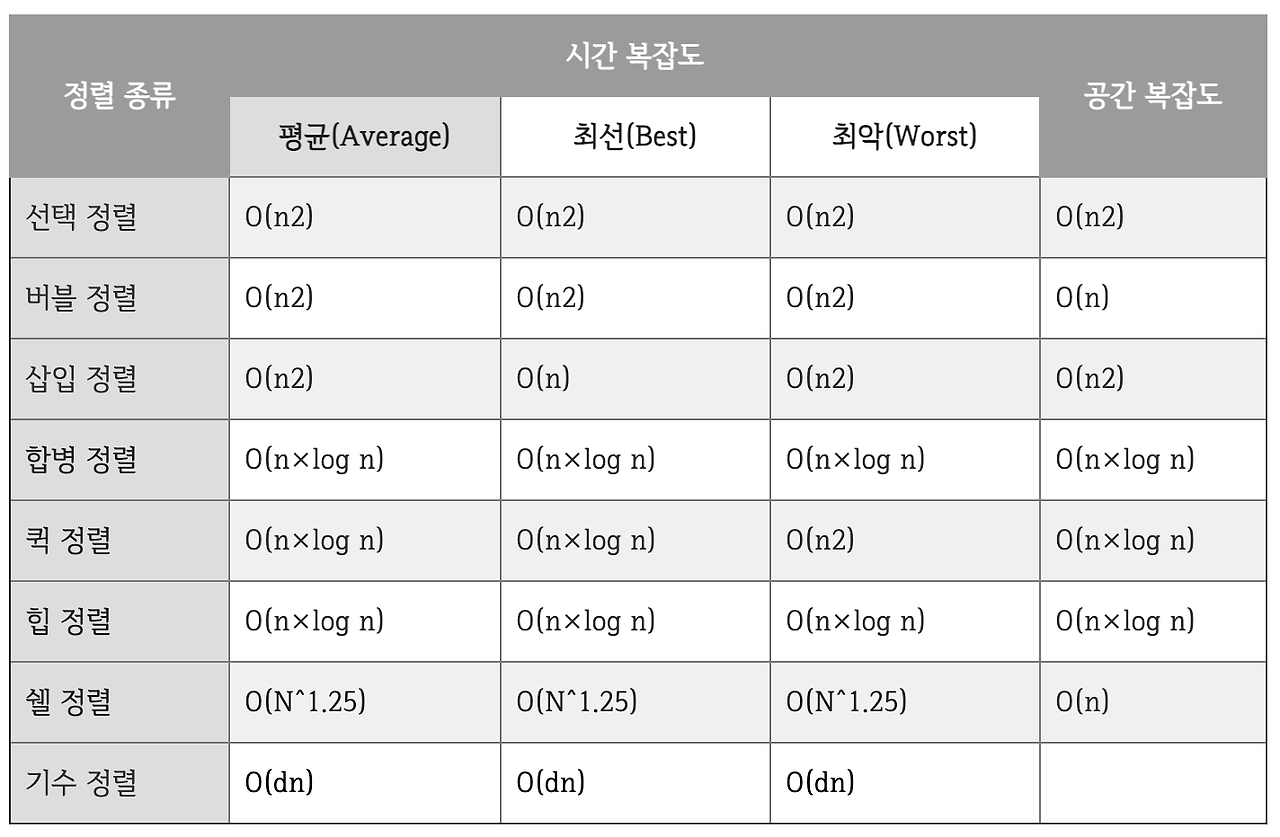
시간 복잡도 표기법
주로 빅오 표기법 O(⋅)을 사용해 알고리즘의 최악의 실행 시간을 표현한다. 알고리즘이 필요로 하는 연산의 수가 데이터 크기 n에 따라 어떻게 증가하는지를 나타낸다
주요 시간 복잡도와 실행 속도 비교
시간 복잡도는 데이터 크기 nn이 클 때 실행 속도가 어떤 식으로 증가하는지에 따라 아래와 같이 분류된다.
1. O(1) - 상수 시간
- 특징: 데이터 크기에 관계없이 항상 일정한 시간에 연산이 완료돼.
- 예시: 배열의 특정 인덱스 접근, 해시 테이블에서 키로 값 찾기.
- 효율성: 매우 빠르며 데이터 크기에 영향을 받지 않아.
2. O(logn) - 로그 시간
- 특징: 데이터 크기가 커져도 실행 시간이 급격히 느려지지 않고, 비교적 완만하게 증가해.
- 예시: 이진 탐색, 균형 잡힌 이진 검색 트리(BST)에서 탐색.
- 효율성: 데이터가 아주 많아도 실행 속도가 빠름. 매우 효율적.
3. O(n) - 선형 시간
- 특징: 데이터 크기가 커질수록 실행 시간도 비례해서 증가해.
- 예시: 배열에서 모든 요소 순회하기, 단순 검색.
- 효율성: 데이터 크기에 따라 시간이 늘어나지만, 비교적 효율적.
4. O(nlogn) - 선형 로그 시간
- 특징: 선형보다 조금 더 빠르지만, 로그 시간보다는 느려.
- 예시: 합병 정렬(Merge Sort), 힙 정렬(Heap Sort), 퀵 정렬(Quick Sort, 평균적인 경우).
- 효율성: 정렬 알고리즘에서 많이 나타나는 복잡도로, 대부분의 정렬 문제에서 빠르고 효율적.
5. O(n2) - 이차 시간
- 특징: 데이터 크기가 커질수록 실행 시간이 제곱 비율로 증가해.
- 예시: 버블 정렬(Bubble Sort), 선택 정렬(Selection Sort), 삽입 정렬(Insertion Sort).
- 효율성: 데이터가 적은 경우에는 괜찮지만, 데이터가 커지면 성능이 급격히 떨어져.
6. O(2n) - 지수 시간
- 특징: 데이터 크기가 증가할수록 실행 시간이 매우 빠르게 증가해.
- 예시: 피보나치 수열 재귀 계산, 완전 탐색을 이용한 조합 문제.
- 효율성: 데이터 크기가 조금만 증가해도 매우 느려지므로, 일반적으로 피해야 함.
7. O(n!) - 계승 시간
- 특징: 데이터 크기가 증가하면 실행 시간이 폭발적으로 증가해.
- 예시: 순열 생성, 여행 판매원 문제(TSP)의 완전 탐색.
- 효율성: 가장 비효율적인 시간 복잡도로, 실질적인 문제 해결에선 사용하기 어려움.

'컴퓨터 일반 > 자료구조론' 카테고리의 다른 글
| 자료구조 문제 정리 (2) 스택, 큐 (0) | 2024.10.25 |
|---|---|
| 자료구조 문제 정리 (1) 배열, 리스트 (4) | 2024.10.25 |
| 선형 자료구조 (0) | 2024.10.24 |
| 자료구조 트리 (3) | 2024.10.23 |
| 그래프 알고리즘 (1) | 2024.10.23 |

